Estática: do Corpo Rígido
| A Estática estuda o equilíbrio dos corpos, ou seja, corpos que estejam parados ou em Movimento Retilíneo Uniforme. Nestes corpos a resultante das forças a eles aplicada é nula. No caso de um corpo possuir dimensões muito pequenas em relação à situação estudada, podemos admitir que ele se comporte como um ponto material e, para que esteja em equilíbrio, basta que a resultante das forças aplicadas seja nula, isto é: ΣF→=0
|
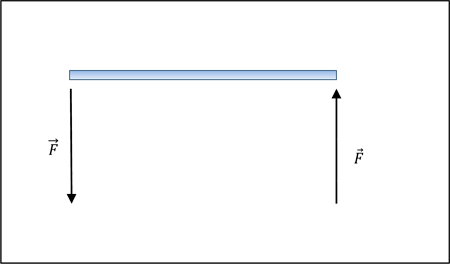
| Porém, se as dimensões do corpo influírem nos resultados do estudo, um novo componente deve ser acrescentado o momento de uma força. Veja o exemplo abaixo: |
| Note que a somatória das forças é nula ( ), mas o corpo se movimenta, pois ele gira. Existe aqui uma nova grandeza, o momento de uma força, que é definido em relação a um determinado ponto. O momento da força será o produto:
M=±F⋅d
|
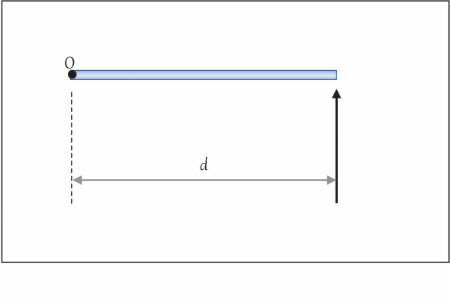
| A unidade de medida do momento de uma força é newton.metro (N.m). A distância d será o braço de alavanca, que é sempre medido na perpendicular à direção da força até o seu ponto de aplicação O. O sinal do momento deve ser definido como positivo ou negativo. Esta definição é arbitrária: por exemplo, vamos definir a tendência do corpo de girar no sentido horário em torno do ponto O como positivo. Neste caso, na figura dada, utilizando este critério, o momento seria negativo. Logo, para um corpo rígido, o sistema de equações para a ocorrência do equilíbrio será:
ΣF→=0
ΣM−→=0
|
| Sendo que a somatória das forças pode ser decomposta em duas direções, x e y:
ΣFx−→=0
ΣFy−→=0
|
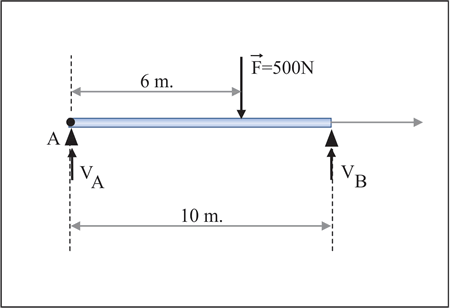
| Por exemplo, imagine uma barra biapoiada conforme a figura:
|
| Onde e são as reações de apoio nos pontos A e B respectivamente. Como não há forças na direção horizontal (x), somente serão consideradas forças verticais (y) com o sentido positivo para cima conforme indicado na figura: ΣFy−→=0
VA+VB−500=0(I)
|
| Adotando-se o sentido horário como positivo e o ponto de giro como sendo A:
ΣM−→=0−10VB=500⋅8=010VB=500VB=50N
|
| Substituindo em (I):
VA+50−500=0VA=450N
|
Fonte: Uol Educação